|
Полезная статья? Пожалуйста, поставьте "+"
Математические методы в экономике - Содержание
Задачей оптимизации в математике,
информатике и исследовании операций называется задача нахождения
экстремума (минимума или максимума) целевой функции в некоторой области
конечномерного векторного пространства, ограниченной набором линейных
и/или нелинейных равенств и/или неравенств.
В процессе проектирования ставится
обычно задача определения наилучших, в некотором смысле, структуры или
значения параметров объектов. Такая задача называется оптимизационной.
Если оптимизация связана с расчетом оптимальных значений параметров при
заданной структуре объекта, то она называется параметрической. Задача
выбора оптимальной структуры является структурной оптимизацией.
Стандартная математическая задача
оптимизации формулируется таким образом. Среди элементов χ, образующих
множества Χ, найти такой элемент χ* , который доставляет минимальное
значение f(χ*) заданной функции f(χ). Для того, чтобы корректно
поставить задачу оптимизации необходимо задать:
- Допустимое множество — множество
 ; ; - Целевую функция — отображение
 ; ; - Критерий поиска (max или min).
Тогда решить задачу 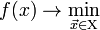 означает одно из: означает одно из:
- Показать, что
 . . - Показать, что целевая функция
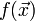 не ограничена снизу. не ограничена снизу. - Найти
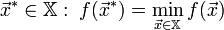 . . - Если
 , то найти , то найти  . .
Если минимизируемая функция не является выпуклой, то часто ограничиваются поиском локальных минимумов и максимумов: точек x0 таких, что всюду в некоторой их окрестности 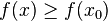 для минимума и для минимума и 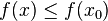 для максимума. для максимума.
Если допустимое множество 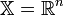 , то такая задача называется задачей безусловной оптимизации, в противном случае — задачей условной оптимизации. , то такая задача называется задачей безусловной оптимизации, в противном случае — задачей условной оптимизации.
Классификация методов оптимизации
Общая
запись задач оптимизации задаёт большое разнообразие их классов. От
класса задачи зависит подбор метода (эффективность её решения).
Классификацию задач определяют: целевая функция и допустимая область
(задаётся системой неравенств и равенств или более сложным алгоритмом).
Методы оптимизации классифицируют в соответствии с задачами оптимизации:
- Локальные методы: сходятся к
какому-нибудь локальному экстремуму целевой функции. В случае
унимодальной целевой функции, этот экстремум единственен, и будет
глобальным максимумом/минимумом.
- Глобальные методы: имеют дело с
многоэкстремальными целевыми функциями. При глобальном поиске основной
задачей является выявление тенденций глобального поведения целевой
функции.
Существующие в настоящее время методы поиска можно разбить на три большие группы:
- детерминированные;
- случайные (стохастические);
- комбинированные.
По критерию размерности допустимого множества, методы оптимизации делят на методы одномерной оптимизации и методы многомерной оптимизации.
По виду целевой функции и допустимого множества, задачи оптимизации и методы их решения можно разделить на следующие классы:
- Задачи оптимизации, в которых целевая функция
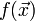 и ограничения и ограничения  являются линейными функциями, разрешаются так называемыми методами линейного программирования. являются линейными функциями, разрешаются так называемыми методами линейного программирования.
- В противном случае имеют дело с
задачей нелинейного программирования и применяют соответствующие методы.
В свою очередь из них выделяют две частные задачи:
- если
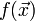 и и  — выпуклые функции, то такую задачу называют задаче выпуклого программирования; — выпуклые функции, то такую задачу называют задаче выпуклого программирования; - если
 , то имеют дело с задачей целочисленного (дискретного) программирования. , то имеют дело с задачей целочисленного (дискретного) программирования.
По требованиям к гладкости и наличию у целевой функции частных производных, их также можно разделить на:
- прямые методы, требующие только вычислений целевой функции в точках приближений;
- методы первого порядка: требуют вычисления первых частных производных функции;
- методы второго порядка: требуют вычисления вторых частных производных, то есть гессиана целевой функции.
Помимо того, оптимизационные методы делятся на следующие группы:
- аналитические методы;
- численные методы;
- графические методы
В зависимости от природы множества X задачи математического программирования классифицируются как:
- задачи дискретного программирования (или комбинаторной оптимизации) — если X конечно или счетно;
- задачи целочисленного программирования — если X является подмножеством множества целых чисел;
- задачей нелинейного программирования, если ограничения или целевая функция содержат нелинейные функции и X является подмножеством конечномерного векторного пространства.
- Если же все ограничения и целевая функция содержат лишь линейные функции, то это — задача линейного программированиея.
Кроме
того, разделами математического программирования являются
параметрические программирование,динамическое
программирование и стохастическое программирование. Математическое
программирование используется при решении оптимизационных
задач исследования операция.
Способ
нахождения экстремума полностью определяется классом задачи. Но перед
тем, как получить математическую модель, нужно выполнить 4 этапа
моделирования:
- Определение границ системы оптимизации
- Отбрасываем те связи объекта
оптимизации с внешним миром, которые не могут сильно повлиять на
результат оптимизации, а, точнее, те, без которых решение упрощается
- Выбор управляемых переменных
- «Замораживаем» значения некоторых
переменных (неуправляемые переменные). Другие оставляем принимать любые
значения из области допустимых решений (управляемые переменные)
- Определение ограничений на управляемые переменные
- … (равенства и\или неравенства)
- Выбор числового критерия оптимизации
| 



